Simulation, Error, and Modeling the Physical World

A few years ago I took a course from Sauro Succi called Computational Methods for the Physical Sciences that surveyed topics such as computational methods for solving partial differential equations, methods for simulating physical systems where processes span different scales of magnitude such as turbulence or fracturing materials, and statistical physics.

Arguably the most interesting feature of the course was the Lattice-Boltzmann method for simulating fluid dynamics that has particular advantages in its efficiency and amenability to parallelization.

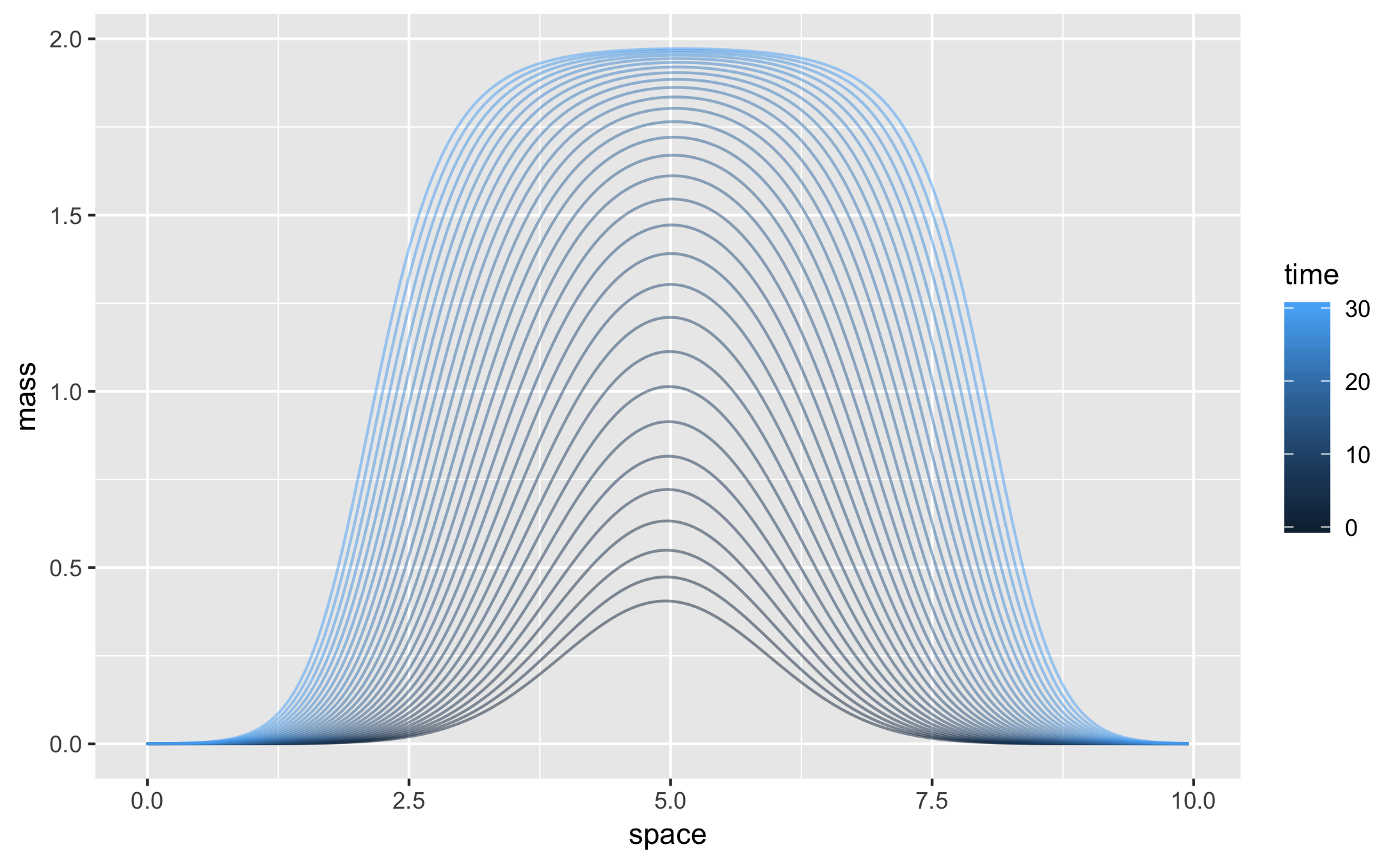
Throughout this course I created a handful of visualizations that, looking back on, seem worth sharing. The first of which, depicted above, shows a normally distributed mass shifting across periodic boundaries on the left and right hand sides as it slowly diffuses and spreads out. There’s nothing deep about this, I just thought the visualization looks nice.

A rectangular distribution of mass is shown in multiple iterations where the edges start to rapidly oscillate due to Gibbs phenomenon in a way that doesn’t reflect what would really happen in reality (the rectangle would just move to the side).

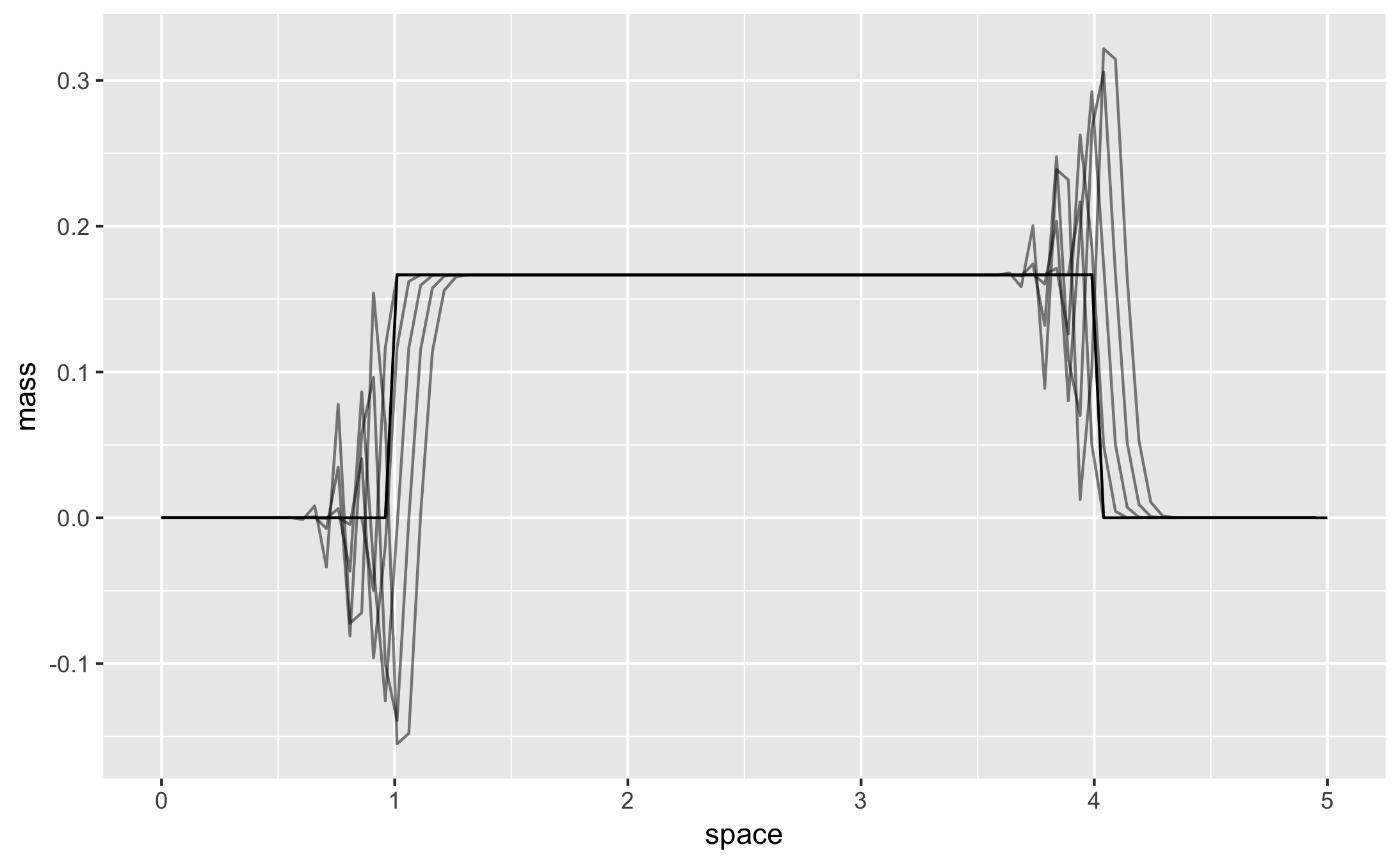
One of the concepts introduced in this course was Gibbs phenomenon which is what happens in a variety of contexts, the most popular of which being when one either attempts to approximate a square distribution through Fourier decomposition, or when one attempts to propogate a square distribution of mass over a discretized model of space. The result is that when the movement does not exactly line up with the discretization of space, the approximation of how much mass is at each discrete point in space can go quite haywire.

A normal distribution is shown “puffing up” after each iteration, eventually appearing as though it has puffed up against an upper limit past which it cannot puff anymore

This is a visualization of some material which can be thought of as reacting with itself in a way that produces more of itself (not realistic, I know) up to the observed carrying capacity. Again, nothing profound, just an aesthetically pleasing visualization.

For my final project in this course, I worked on a spatial model of infectious disease transmission with stochasticity and reinfection. I think infectious disease modeling is a fascinating subject and I’m suspicious it’s worth thinking through the intricacies of how stochasticity can affect disease dynamics in ways that deterministic equations might not reveal.